二叉搜索树

Posted on 2025-04-02 Edited on 2025-05-12 In data_structure Views:

[TOC]

红黑树

红黑树的定义：

每个节点为红色或黑色。

根节点始终为黑色。

红色节点的子节点必须为黑色（无连续红色节点）。

从根到每个叶节点（NIL节点）的黑色节点数量（黑色高度）相等。

所有叶节点（NIL节点）为黑色。

通过红黑树的定义，可确保其没有一条路径长度能够超出其他路径的2倍。通过下图可知，因为需要保证从根到每个叶节点的黑色节点数量（黑色高度）相等，所以左侧为black -> red -> black -> red -> black -> null 右侧为black -> black -> black -> null从根节点到NIL节点（图中标为NULL）都只有三个，两者高度相差相差是小于2倍的。

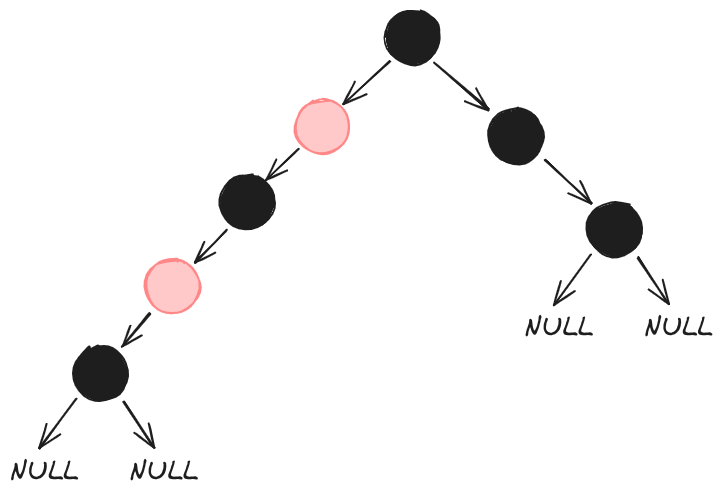
红黑树控制了最长路径和最短路径之比，间接地使红黑树达到了“近似平衡”，增删查改地时间消耗不会过大，并且相比AVL树，旋转调整次数会更少。

红黑树节点的数据结构

class RBNode<K extends Comparable<K>, V> {
    K key;
    V value;
    RBNode<K, V> parent, leftChild, rightChild;
    boolean isRed;

    public RBNode(K key, V value, RBNode<K, V> leftChild, RBNode<K, V> rightChild, RBNode<K, V> parent, boolean isRed) {
        this.key = key;
        this.value = value;
        this.leftChild = leftChild;
        this.rightChild = rightChild;
        this.parent = parent;
        this.isRed = isRed;
    }
}

红黑树的插入

为了不影响红黑树中黑色数量的平衡，将插入的节点默认设置为红色，但插入红色后会出现双红的情况，需进行调整。

情况1：root是空

直接插入到root并设置为黑色

情况2：root不为空

根据二叉树找到需要插入的位置，即某个叶子节点(NIL)并记录它的父节点(p)

情况2.1：父节点(p)为黑色

直接在该叶子节点(NIL)插入并设置为红色

情况2.1：父节点(p)为红色

若加入红色的插入节点，会出现双红的情况。

情况2.1.1：父节点(p)的兄弟节点(u)为黑色或(NIL)

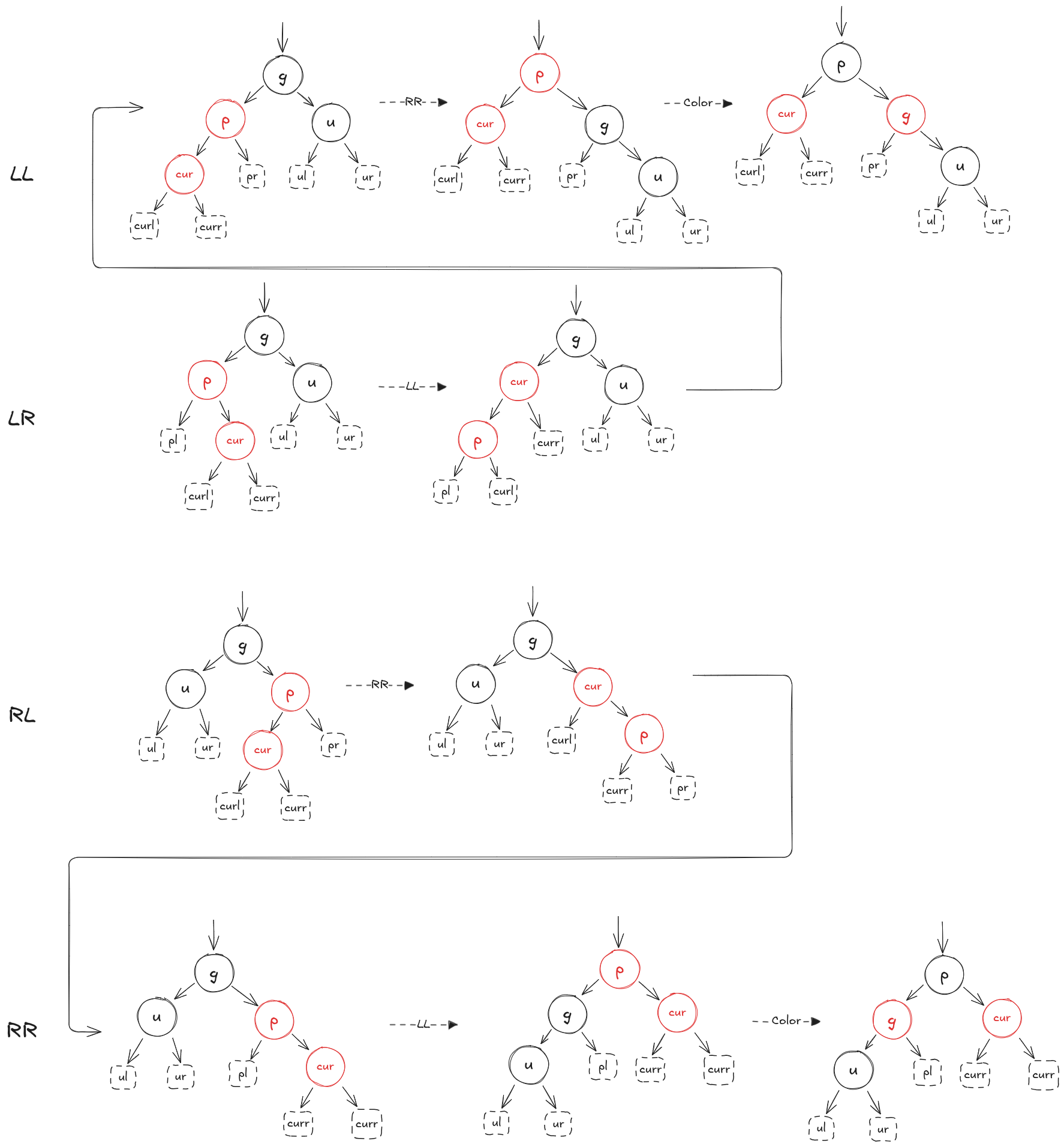
父节点(p)的兄弟节点(u)也就是插入节点(cur)的叔叔节点。该情况共有四种情况：

(p)是(g)的左儿子，(cur)是(p)的左儿子，执行LL情况
(p)是(g)的左儿子，(cur)是(p)的右儿子，执行LR情况
(p)是(g)的右儿子，(cur)是(p)的左儿子，执行RL情况
(p)是(g)的右儿子，(cur)是(p)的右儿子，执行RR情况

LL情况：

算法：

对(p)节点右旋
重新着色： (p)设置为黑色，(g)设置为红色
结束

分析（其他情况类推）：

若下图是红黑树的最底层叶子节点，则(curl) = NIL, (curr) = NIL, (pr) = NIL, (u) = NIL。所以旋转结束后，以(p)为根节点的子树黑色平衡且高度为一没有发生变化。

若下图是递归迭代过程中，并假设(u)存在，如果不存在就变为上面红黑树的最底层的情况一致了。那么(g)的右子树黑色高度为 [1 + (u)子树黑色高度] 为保持平衡，(pr)中黑色节点的高度为 [1 + (u)子树黑色高度]也就是至少有一个黑色节点，(curl)与(curr)跟(pr)是一样的。在旋转后，(curl)(curr)(pr)的黑色高度都为 [1 + (u)子树黑色高度]，(g)的右子树黑色高度也是 [1 + (u)子树黑色高度] 所以旋转后黑色仍然平衡且没有发生变化。

无论是红黑树的最底层叶子节点还是递归迭代过程中，旋转变色之后黑色都是平衡且高度不变的，并且子树的根节点为黑色不变。故不需要向上调整。

LR情况：

算法：

对(cur)节点左旋
变为LL情况，按照LL情况执行后续操作

RR情况：

算法：

对(p)节点左旋
重新着色： (p)设置为黑色，(g)设置为红色
结束

RL情况：

算法：

对(cur)节点右旋
变为RR情况，按照RR情况执行后续操作

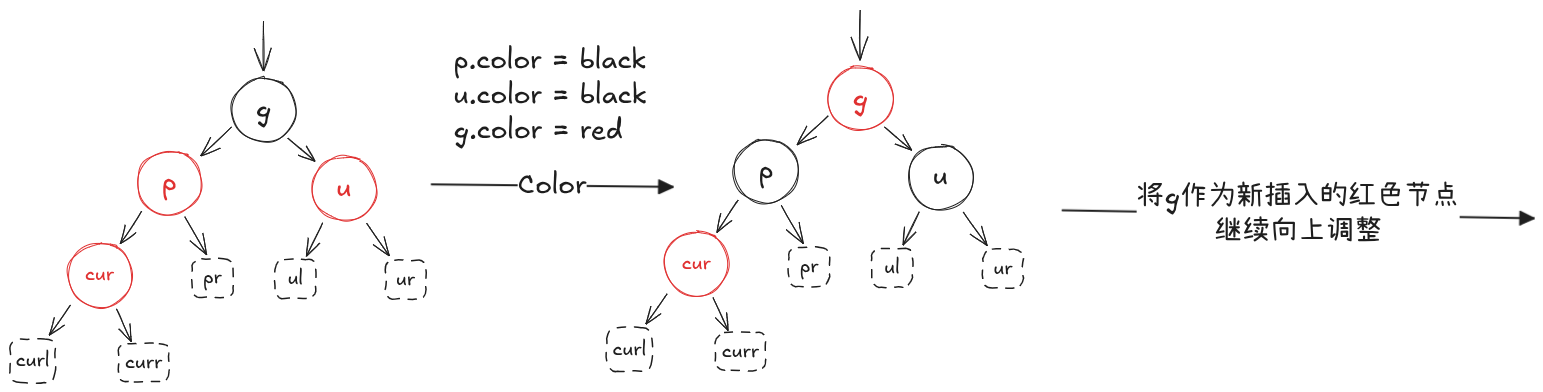
情况2.1.2：父节点(p)的兄弟节点(u)为红色

算法：

重新着色：(p)设置为黑色，(u)设置为黑色，(g)设置为红色
将(g)看作新插入的红色节点，向上递归迭代。一直迭代到根节点即(g)为root，将(g)改为黑色，直接结束。

红黑树的删除

首先要明确几个概念：

1.约定(NIL)是黑色，也可以作为实际节点的儿子。

旋转操作包括左旋和右旋

2.左旋：

本文以(cur)为基点进行旋转（有些文章是以(p)为基点）

算法：

记录节点(p)的父节点(g)（如果有），图中并为标出
将节点(curl)移至节点(p)的右儿子
将节点(p)移至节点(cur)的左儿子
将节点(cur)移至节点(g)的儿子指向，（如果节点(p)有父节点(g)）

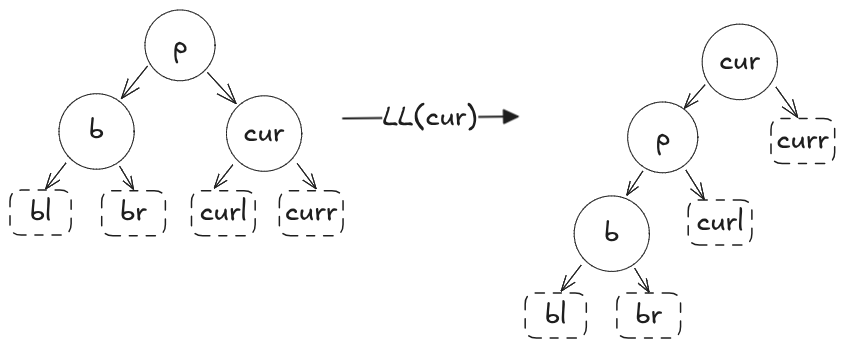
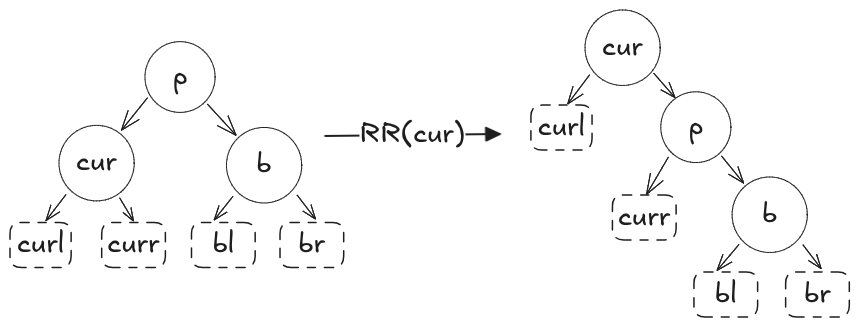
3.右旋：

本文以(cur)为基点进行旋转（有些文章是以(p)为基点）

算法：

记录节点(p)的父节点(g)（如果有），图中并为标出
将节点(curr)移至节点(p)的左儿子
将节点(p)移至节点(cur)的右儿子
将节点(cur)移至节点(g)的儿子指向，（如果节点(p)有父节点(g)）

4.删除节点

针对删除操作，不同的文章有不同的标准，有直接删除节点的，有定义双黑节点的。本文会结合两者。

为了更直观的观察节点的删除情况，本文以直接删除节点的情况来绘图，但删除过程中有一种情况需要递归向上的平衡子树，所以在递归的情况下，使用双黑节点。无论使用直接删除节点还是双黑节点，两者的原理是相同的。

代码实现中：在寻找到删除节点后（该节点是经过移动后最终的删除节点没有儿子的情况）便立刻用(NIL)替代删除节点，后续判断过程中无论是最底层节点的直接删除，还是递归向上平衡子树都不需要再次删除了，即相当于使用的是双黑节点的思路，即双黑节点的内容是删除后的最后结果，不需要再操作了，只需要平衡该节点即可。

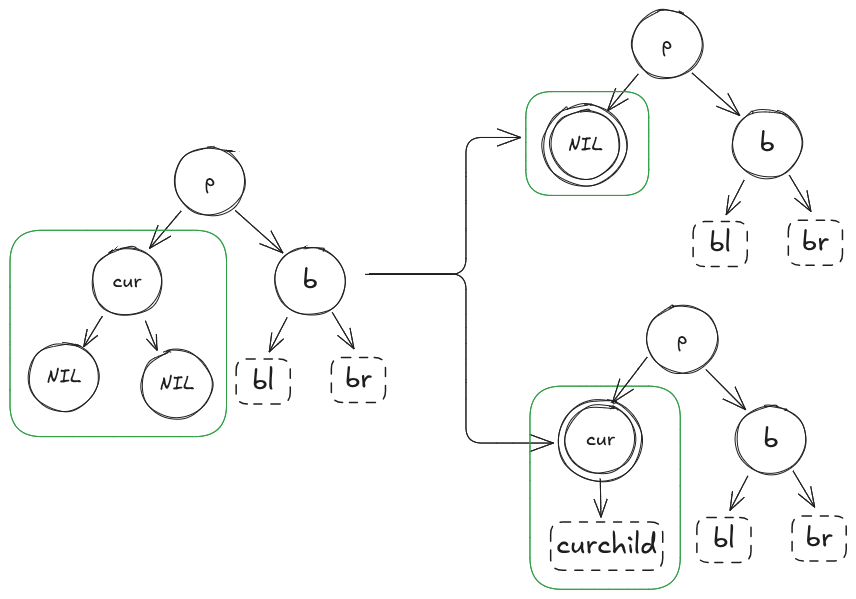
下图中要删除的节点是(cur)：

若(cur)没有子节点则它的两个儿子都是NIL节点，删除后需要用(NIL)替代。右上子树是其双黑节点的表示形式
若(cur)有子节点，这种情况只出现在递归向上平衡子树的情况中，该情况在图中用双黑节点表示，但是旋转变色过程与直接删除节点的情况是一样的。右下子树是其双黑节点的表现形式。

这三种表现形式都是一样的，都是以(cur)节点为根的子树内部的不同表现形式，并不会影响到(p)以及上面的节点。

5.图标

黑圆代表黑色节点，红圆代表红色节点，虚线圆代表红或者黑节点。

双圆代表双黑节点

黑方形代表根是黑色的子树，红方形代表根是红色的子树，虚线方形代表根是黑色或者红色的子树。其中子树可能是(NIL)，可能只有一个节点，也可能有多层。

删除原理： 首先通过二叉树搜索找到需要删除的节点(cur)，若节点为红色用其某个儿子节点替代即可。若节点为黑色，删除该节点会导致黑色节点数量减一，导致黑色节点数量不再平衡，为了保证删除后仍然黑色平衡，需要借用一个红色节点转移到该子树上变为黑色，这样该子树的黑色节点数量和删除之前是一样的，根据不同的情况，该红色节点可以从删除节点(cur)的孩子上，兄弟节点(b)的子树上、父节点(p)以其上面祖辈这三个地方借用红色。

注：其中双黑节点就是删除原节点后黑色高度减一的子树的根，等借一个红节点变为黑色后黑色高度平衡，即可将该双黑节点改为单黑节点（即正常黑色节点）

首先通过二叉树搜索找到需要删除的节点(cur)，根据(cur)的孩子节点情况分类：

(cur)有两个儿子节点
(cur)有一个儿子节点
(cur)没有儿子节点

情况1：(cur)有两个儿子节点

找到(cur)节点的前驱节点或后继节点来替代(cur)节点，替代后颜色设置为(cur)节点的颜色，然后继续删除该前驱节点或后继节点。本文采用后继节点来替代删除节点(cur)

情况2：(cur)有一个儿子节点

(cur)有一个儿子节点有两种可能：

情况2.1：(cur)是红色（不存在）

当(cur)是红色且它有一个儿子节点。若儿子节点是黑色，则黑色数量不平衡；若儿子节点是红色，则两个红色不能为父子。所以该情况不存在。

情况2.2：(cur)是黑色

当(cur)是黑色且它有一个儿子节点。若儿子节点是黑色，则黑色数量不平衡；若儿子节点是红色，成立。

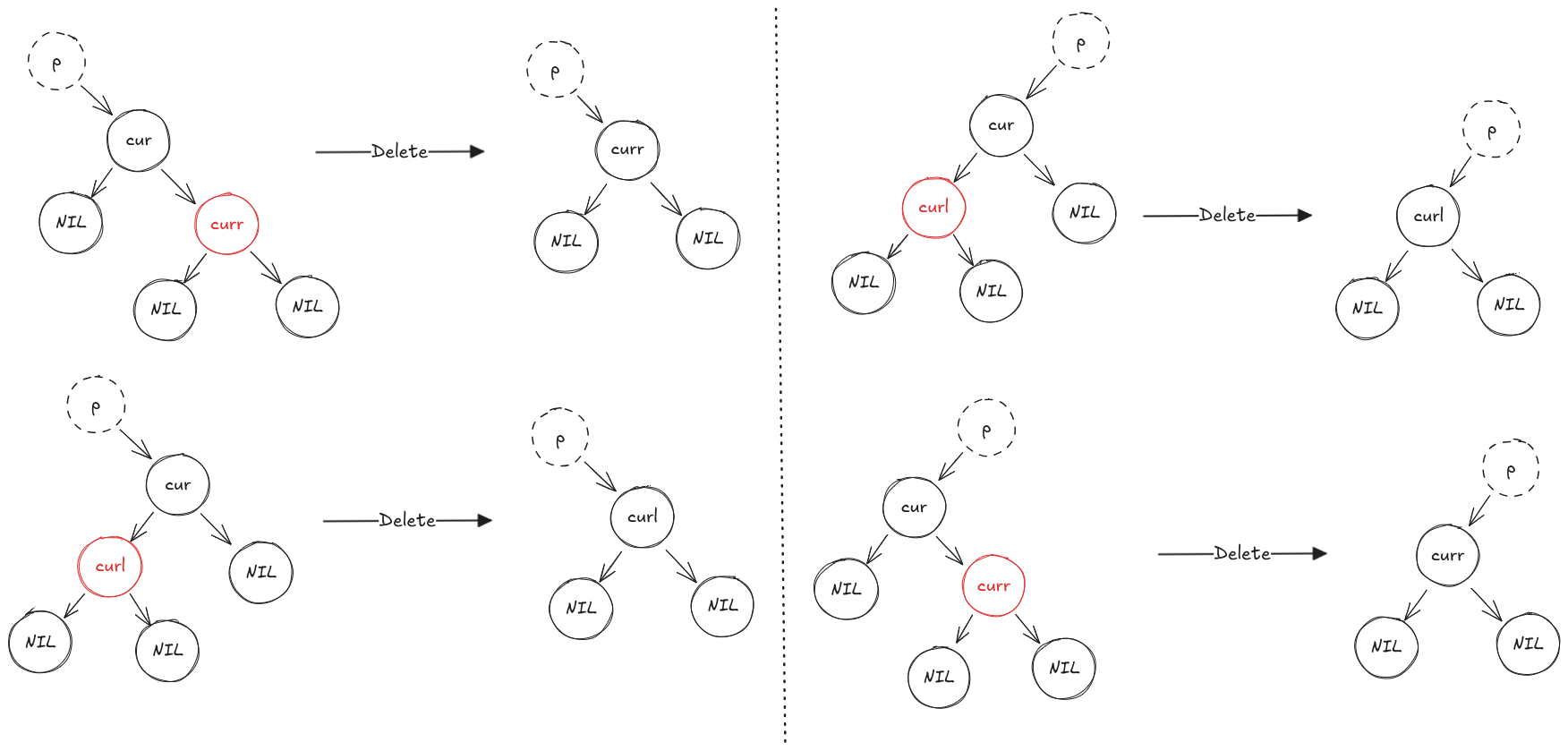
该情况只有(cur)是黑色，(cur)的一个儿子是红色。因为自己的儿子就是红色，可以像自己的儿子借红色节点。

算法：

将(cur)节点的红色儿子替代(cur)节点。即(p)节点的儿子换为(cur)节点的红色儿子（如果(p)存在）
将(cur)节点红色儿子的颜色改为(cur)的颜色，即黑色

情况3：(cur)没有儿子节点

(cur)没有儿子节点分为两种情况：

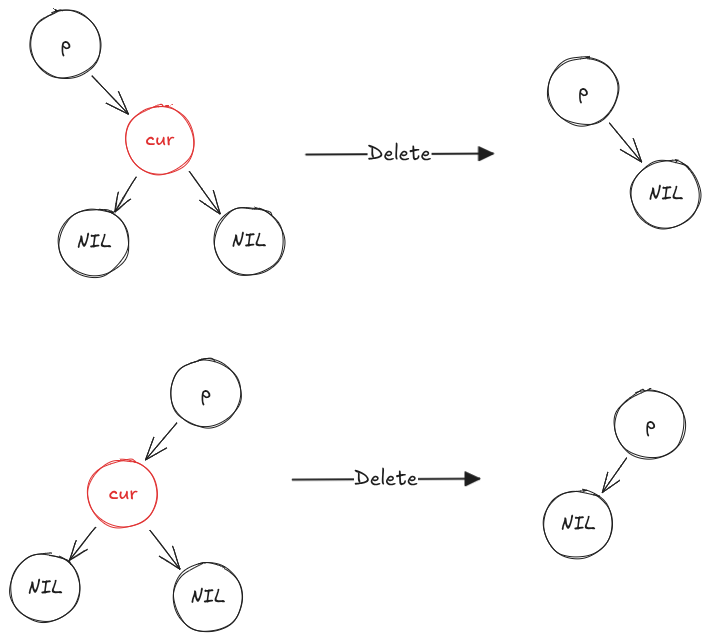
情况3.1：(cur)是红色

(cur)是红色且没有儿子节点，直接删除该节点用(NIL)替代即可。因为删除红色节点并不会影响黑色平衡。

算法：

用(NIL)节点替代(cur)节点，即(p)节点的儿子换为(cur)节点的(NIL)节点（如果(p)存在）

情况3.2：(cur)是黑色

(cur)是黑色，删除后会导致(cur)锁在的原子树黑色高度减一，所以需要借红色节点变为黑色来补齐黑色高度，而(cur)没有孩子节点，此时需要向兄弟节点或者父亲节点来借。

情况3.2.1：(cur)的兄弟节点(b)是黑色，且(b)的外节点儿子是红色

当(cur)是(p)的左儿子，(b)为(p)的右儿子

算法：

对兄弟节点(b)左旋
重新着色：(br)设置为黑色，(b)设置为(p)的颜色，(p)设置为黑色
删除(cur)节点，用(NIL)替代；若是递归过程中，(cur)节点已经替代过了，不需要操作，以双黑的话术是一开始即用 (NIL) 或 (cur)自身 替代(cur)形成双黑节点，此时将双黑节点变为单黑（即正常的黑色节点）

完成操作后，以(b)为根节点的子树黑色平衡且高度与原来一致，结束平衡过程。

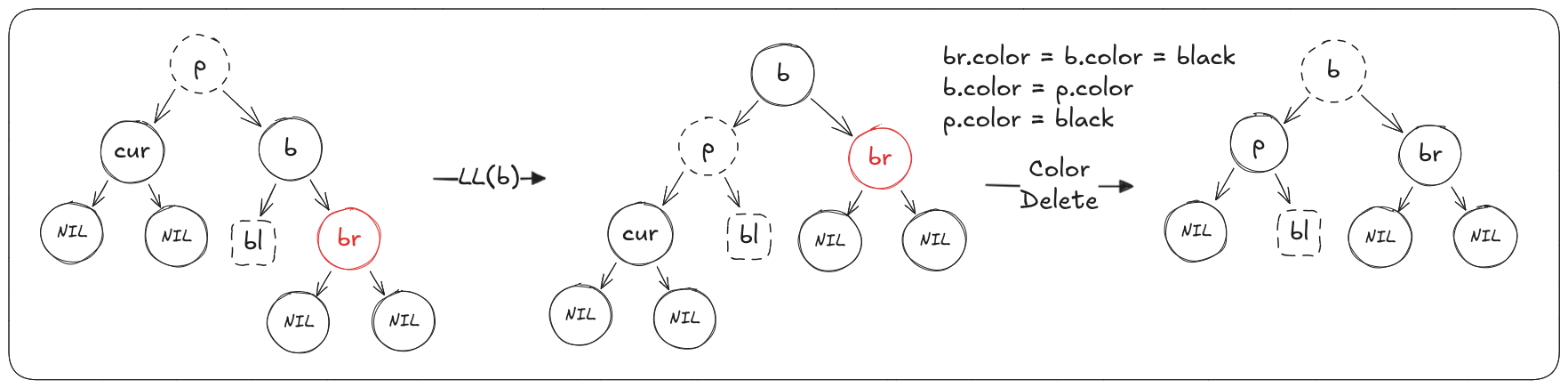
当(cur)是(p)的右儿子，(b)为(p)的左儿子

算法：

对兄弟节点(b)右旋转
重新着色：(bl)设置为黑色，(b)设置为(p)的颜色，(p)设置为黑色
删除(cur)节点，用(NIL)替代；若是递归过程中，(cur)节点已经替代过了，不需要操作，以双黑的话术是一开始即用**(NIL)或(cur)自身**替代(cur)形成双黑节点，此时将双黑节点变为单黑（即正常的黑色节点）

完成操作后，以(b)为根节点的子树黑色平衡且黑色高度与原来一致且**(b)的颜色与原来根节点(p)颜色相同**，结束平衡过程。

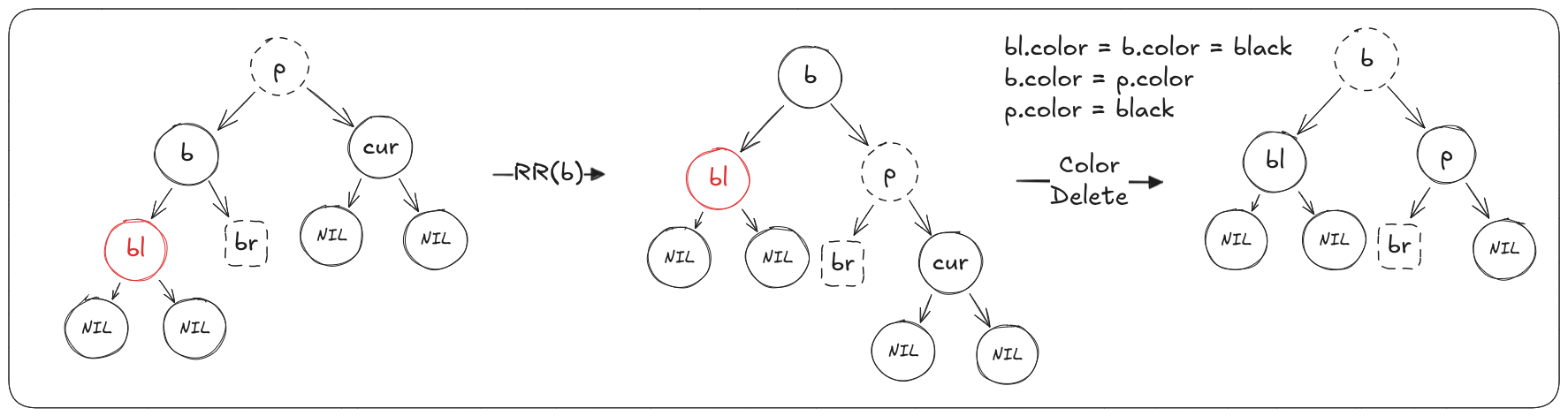
情况3.2.2：(cur)的兄弟节点(b)是黑色，且(b)的内节点儿子是红色（其外节点儿子是黑色）

当(cur)是(p)的左儿子，(b)为(p)的右儿子

算法：

对(bl)节点进行右旋
再对(bl)节点进行左旋
重新着色：(bl)设置为(p)的颜色，(p)设置为黑色
删除(cur)节点，用(NIL)替代；若是递归过程中，(cur)节点已经替代过了，不需要操作，以双黑的话术是一开始即用**(NIL)或(cur)自身**替代(cur)形成双黑节点，此时将双黑节点变为单黑（即正常的黑色节点）

完成操作后，以(bl)为根节点的子树黑色平衡且黑色高度与原来一致且**(bl)的颜色与原来根节点(p)颜色相同**，结束平衡过程。

当(cur)是(p)的右儿子，(b)为(p)的左儿子

算法：

对(br)节点进行左旋
再对(br)节点进行右旋
重新着色：(br)设置为(p)的颜色，(p)设置为黑色
删除(cur)节点，用(NIL)替代；若是递归过程中，(cur)节点已经替代过了，不需要操作，以双黑的话术是一开始即用**(NIL)或(cur)自身**替代(cur)形成双黑节点，此时将双黑节点变为单黑（即正常的黑色节点）

完成操作后，以(br)为根节点的子树黑色平衡且黑色高度与原来一致且**(br)的颜色与原来根节点(p)颜色相同**，结束平衡过程。

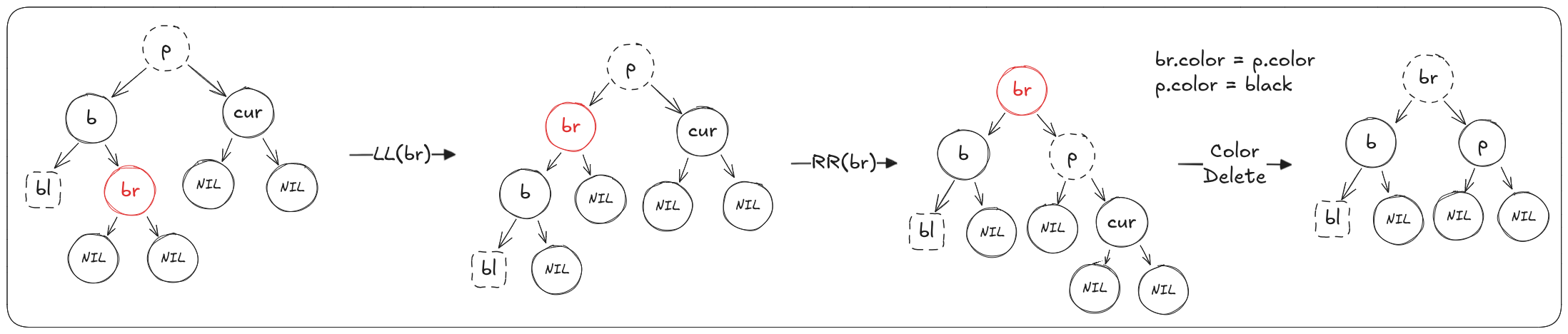
情况3.2.3：(cur)的兄弟节点(b)是黑色，且(b)的两个儿子都是黑色

该情况下，(b) (bl) (br) (cur)均为黑色

情况3.2.3.1: 父节点(p)为红色

算法：

重新着色：(p)设置为黑色，(b)设置为红色
删除(cur)节点，用(NIL)替代；若是递归过程中，(cur)节点已经替代过了，不需要操作，以双黑的话术是一开始即用**(NIL)或(cur)自身**替代(cur)形成双黑节点，此时将双黑节点变为单黑（即正常的黑色节点）

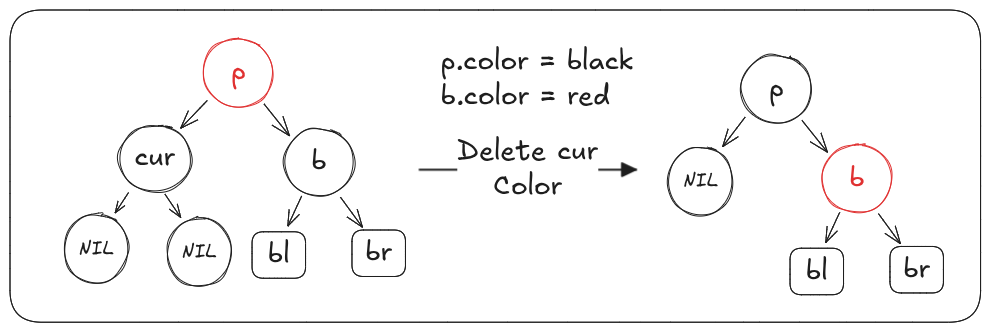
完成操作后，以(p)为根节点的子树黑色平衡且黑色高度与原来一致且(p)为黑色不会与其父节点冲突，结束平衡过程。

情况3.2.3.2: 父节点(p)为黑色

算法：

重新着色：(b)设置为红色
删除(cur)节点，用(NIL)替代；若是递归过程中，(cur)节点已经替代过了，不需要操作，以双黑的话术是一开始即用**(NIL)或(cur)自身**替代(cur)形成双黑节点，此时将双黑节点变为单黑（即正常的黑色节点）
将(p)设为双黑节点，递归向上继续平衡(p)，向上平衡过程中需要以下图规定的顺序进行判断，若都不满足需要将(p)的父节点设为双黑，继续向上平衡。若(b)为根节点，即(p)为NULL，终止递归。

完成操作后，以(p)为根节点的子树黑色平衡 但 黑色高度减少了一，所以需要继续向上平衡(p)节点。此时可以将以(p)为根节点的子树看作一个整体，在以(pp)为根节点的子树中平衡，如果以(pp)为根节点的子树仍然不能平衡，就继续向上迭代，直至整棵树的根节点结束。

递归判断顺序：

(bb)为黑色且(bbr)为红色
(bb)为黑色且(bbl)为红色
(bb)为红色
(bb)为黑色且(bbl)和(bbr)均为黑色且(pp)为红色

若上述条件都不满足即出现了**(bb)为黑色且(bbl)和(bbr)均为黑色且(pp)为黑色**，这时需要继续平衡(pp)节点，即将(pp)设置为双黑节点，继续向上递归。一直递归到(pp)节点为NULL

情况3.2.4：(cur)的兄弟节点(b)是红色

该情况下(p)一定是黑色，(bl)和(br)一定是黑色

当(cur)是(p)的左儿子，(b)为(p)的右儿子

算法：

对(b)进行左旋
重新着色：(b)设置为黑色，(p)设置为红色
平衡以(p)为根节点的子树，继续平衡(cur)，此时变为了兄弟节点是黑色的情况。平衡结束即全部结束

在以(p)为根节点的子树中，可能出现三种情况：

(blr)是红色，执行情况3.2.1：(cur)的兄弟节点(b)是黑色，且(b)的外节点儿子是红色
(bll)是红色且(blr)是黑色，执行情况3.2.2：(cur)的兄弟节点(b)是黑色，且(b)的内节点儿子是红色（其外节点儿子是黑色）
(bll)是黑色且(blr)是黑色，执行情况3.2.3：(cur)的兄弟节点(b)是黑色，且(b)的儿子都是黑色） 中 (p)为红色 的情况

这三种情况都是可以完成平衡的，不需要递归。

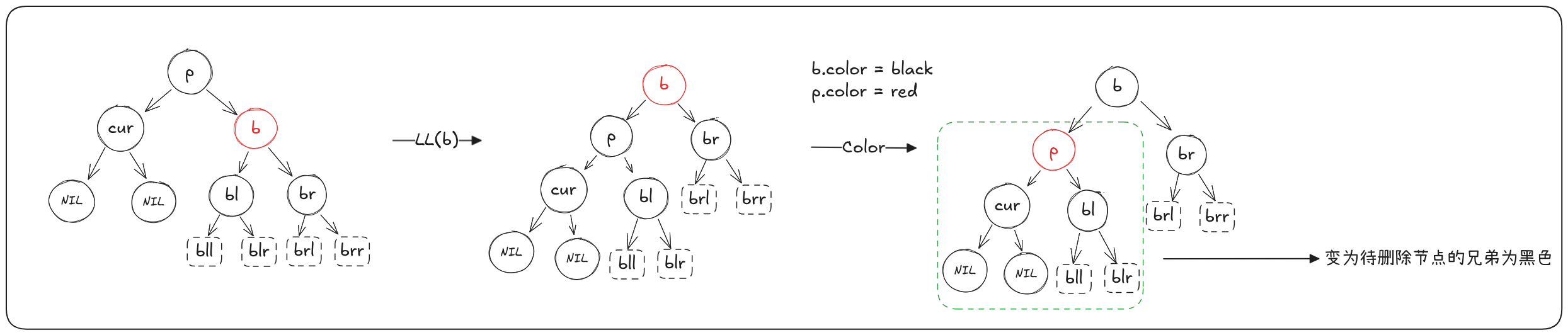
当(cur)是(p)的右儿子，(b)为(p)的左儿子

算法：

对(b)进行右旋
重新着色：(b)设置为黑色，(p)设置为红色
平衡以(p)为根节点的子树，继续平衡(cur)，此时变为了兄弟节点是黑色的情况。平衡结束即全部结束

在以(p)为根节点的子树中，可能出现三种情况：

(brl)是红色，执行情况3.2.1：(cur)的兄弟节点(b)是黑色，且(b)的外节点儿子是红色
(brr)是红色且(brl)是黑色，执行情况3.2.2：(cur)的兄弟节点(b)是黑色，且(b)的内节点儿子是红色（其外节点儿子是黑色）
(brl)是黑色且(brr)是黑色，执行情况3.2.3：(cur)的兄弟节点(b)是黑色，且(b)的儿子都是黑色） 中 (p)为红色 的情况

这三种情况都是可以完成平衡的，不需要递归。

情况3.2.5：(cur)的兄弟节点(b)是(NIL) （不存在）

因为(cur)是黑色，若兄弟节点(b)是(NIL)，则黑色数量不平衡，不存在。

删除总结

至此所有的删除情况都讨论完了。目前规定一下在代码中的情况3.2：(cur)没有子节点是黑色的判断顺序：

情况3.2.1：(cur)的兄弟节点(b)是黑色，且(b)的外节点儿子是红色 [可完成平衡]
情况3.2.2：(cur)的兄弟节点(b)是黑色，且(b)的内节点儿子是红色（其外节点儿子是黑色） [可完成平衡]
情况3.2.4：(cur)的兄弟节点(b)是红色 [可完成平衡]
情况3.2.3：(cur)的兄弟节点(b)是黑色，且(b)的两个儿子都是黑色 中的 **情况3.2.3.1: 父节点(p)为红色 **[可完成平衡]
情况3.2.3：(cur)的兄弟节点(b)是黑色，且(b)的两个儿子都是黑色 中的 情况3.2.3.2: 父节点(p)为黑色 [需向上递归完成平衡]

所有的情况中只有情况3.2.3：(cur)的兄弟节点(b)是黑色，且(b)的两个儿子都是黑色 中的 情况3.2.3.2: 父节点(p)为黑色是需要向上递归完成平衡的。情况3.2.4：(cur)的兄弟节点(b)是红色 只需要转化为 情况3.2：(cur)没有子节点是黑色 中的 情况3.2.1 或 情况3.2.2 或 情况3.2.3中的一种，都可直接完成平衡操作。

情况3.2：(cur)没有子节点是黑色的总结：

兄弟节点为红色：通过旋转和颜色交换，转化为黑色兄弟节点的情况。
兄弟节点为黑色：
- 两个子节点均为黑色：将兄弟设为红色，传播双黑或利用红色父节点解决。
- 远子节点为红色：通过单次旋转和颜色调整消除双黑。
- 近子节点为红色：通过两次旋转和颜色调整消除双黑。

红黑树

红黑树节点的数据结构

红黑树的插入

情况1：root是空

情况2：root不为空

情况2.1：父节点(p)为黑色

情况2.1：父节点(p)为红色

情况2.1.1：父节点(p)的兄弟节点(u)为黑色或(NIL)

情况2.1.2：父节点(p)的兄弟节点(u)为红色

红黑树的删除

情况1：(cur)有两个儿子节点

情况2：(cur)有一个儿子节点

情况2.1：(cur)是红色 （不存在）

情况2.2：(cur)是黑色

情况3：(cur)没有儿子节点

情况3.1：(cur)是红色

情况3.2：(cur)是黑色

情况3.2.1：(cur)的兄弟节点(b)是黑色，且(b)的外节点儿子是红色

情况3.2.2：(cur)的兄弟节点(b)是黑色，且(b)的内节点儿子是红色（其外节点儿子是黑色）

情况3.2.3：(cur)的兄弟节点(b)是黑色，且(b)的两个儿子都是黑色

情况3.2.3.1: 父节点(p)为红色

情况3.2.3.2: 父节点(p)为黑色

情况3.2.4：(cur)的兄弟节点(b)是红色

情况3.2.5：(cur)的兄弟节点(b)是(NIL) （不存在）

删除总结

情况2.1：(cur)是红色（不存在）