贪心算法

Posted on Edited on In Views:

贪心算法

贪心算法或贪心思想采用贪心的策略，保证每次操作都是局部最优的，从而使最后得到的结果是全局最优的。

分配问题

455. 分发饼干

贪心+双指针+排序

为了让尽可能多的孩子得到满足，所以让能满足的孩子所给的饼干尺寸与胃口值尽可能的接近，防止浪费。即把大于等于这个孩子饥饿度的、且大小最小的饼干给这个孩子。

先用小的饼干满足了胃口最小的孩子，然后逐渐满足胃口大的孩子。

算法思想：

  • 对胃口值和饼干尺寸升序排序
  • 从小到大逐个对胃口值进行满足，从小到大寻找第一个满足的饼干尺寸
  • 等遍历到完最后一个饼干或者满足所有的胃口值结束

算法实现：

  • 排序使用Java的Arrays.sort() 算法复杂度 $O(nlog(n))$
  • 对两个数组进行联动遍历，可使用双指针分别指向胃口值数组和饼干尺寸数组
  • 使用while循环遍历
1
2
3
4
5
6
7
8
9
10
11
12
public int findContentChildren(int[] g, int[] s) {
    Arrays.sort(g);
    Arrays.sort(s);
    int gindex = 0, sindex = 0;
    while (sindex < s.length && gindex < g.length) {
        if (g[gindex] <= s[sindex]) {
            gindex++;
        }
        sindex++;
    }
    return gindex;
}

135. 分发糖果

贪心

所有的孩子站成一排，满足相邻两个孩子评分更高的孩子获得更多的糖果，即第$i$个孩子需要与相邻的两个孩子（即第$i-1$,和第$i+1$ 个孩子）进行比较。

贪心算法时将一个复杂的问题分解为多个局部问题，实现局部最优解，最后实现全局最优。

将与左右孩子的比较划分为向右遍历和向左遍历。

算法思想：

向右遍历：从左向右，保证右侧评分大于左侧评分的孩子获得的糖果多，即当$ratings[i+1]>ratings[i]$则$candys[i+1]>candys[i]$

向左遍历：从右向左，保证左侧评分大于右侧评分的孩子获得的糖果多，即当$ratings[i]>ratings[i+1]$则$candys[i]>candys[i+1]$

算法实现：

  • 将candys[]数组全部赋值为1，因为每个孩子至少获取一个糖果

  • 向右遍历：

$$
candys[i+1] = candys[i] + 1 \quad if ratings[i+1] > ratings[i]
$$

  • 向左遍历：
    $$
    candys[i] = max(candy[i], candy[i+1]+1) \quad if \quad ratings[i]> ratings[i+1]
    $$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int candy(int[] ratings) {
    int[] candy = new int[ratings.length];
    Arrays.fill(candy, 1);
    for (int i = 0; i < ratings.length - 1; i++) {
        if (ratings[i] < ratings[i + 1]) {
            candy[i + 1] = candy[i] + 1;
        }
    }
    for (int i = ratings.length - 2; i >= 0; i--) {
        if (ratings[i] > ratings[i + 1]) {
            candy[i] = Math.max(candy[i], candy[i + 1] + 1);
        }
    }
    return Arrays.stream(candy).sum();
}

区间问题

435. 无重叠区间

贪心

要保证移除的区间数量最少，就相当于留下的区间尽可能的多。贪心思路是选择区间的结尾越小，剩余留给其他区间的空间就越大。

算法思想：

从结尾最小的区间开始遍历，去掉与其交叉的所有区间，再选择剩余中结尾最小的区间，重复操作。

算法实现：

  • 将intervals根据先结尾后开头的排序规则对其进行升序排序
  • 选取第一个区间，遍历找出一个区间开头大于等于第一个区间结尾的区间
  • 选取该区间，再去寻找下一个一个区间开头大于等于该区间结尾的区间
  • 依次循环
1
2
3
4
5
6
7
8
9
10
11
12
13
public int eraseOverlapIntervals(int[][] intervals) {
    Arrays.sort(intervals, (a, b) -> a[1] == b[1] ? a[0] - b[0] : a[1] - b[1]);
    int ans = 0;
    int curEnd = intervals[0][1];
    for (int i = 1; i < intervals.length; i++) {
        if (intervals[i][0] < curEnd) {
            ans++;
        } else {
            curEnd = intervals[i][1];
        }
    }
    return ans;
}

452 用最少数量的箭引爆气球

因为要扎爆所有的气球，所以每一箭需要射中尽可能多的气球。当箭射在气球的右边缘时，既能射爆该气球，又能尽可能的覆盖它后面的气球，所以每个气球的右端点很重要。

算法实现：

  1. 将所有的气球升序排序（先排右端点，若右端点相同，再根据左端点）

  2. 选择第一个气球，以其右端点为界，依次向后寻找左端点小于该边界的气球，直至找到左端点大于该边界的气球

  3. 对该气球重复第二步操作，直至扫完所有气球

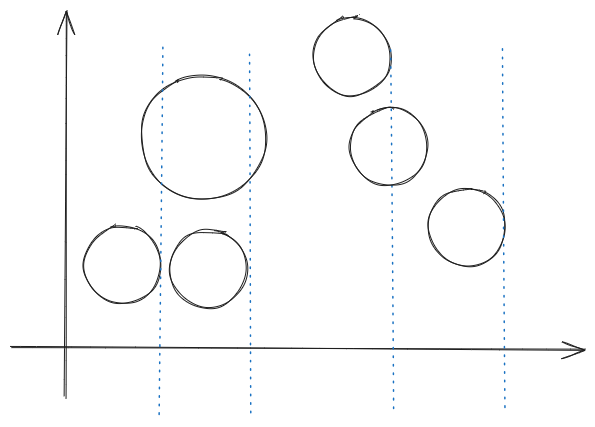
如下图所示，第一个蓝色边界是第一个气球的右端点，会将第一个球和上面的大球射爆。（但在顺序扫描中，第二个小气球会先出现，因为是根据右端点排序，此时第一个边界没有碰到第二个小气球，所以边界更新为第二条蓝色边界，这时下一个气球就是上面的大球，发现大球的左端点是小于目前的第二条蓝色边界的，所以继续向后搜索，相当于此时才将大气球扎爆。虽然看着有些问题，但并不影响根本）

image-20250303192530005

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int findMinArrowShots(int[][] points) {
    Arrays.sort(points, (o1, o2) -> {
        if (o1[1] != o2[1]) {
            return Integer.compare(o1[1], o2[1]);
        } else {
            return Integer.compare(o1[0], o2[0]);
        }
    });
    int ans = 1;
    for (int i = 1, curPoint = points[0][1]; i < points.length; i++) {
        if (points[i][0] > curPoint) {
            curPoint = points[i][1];
            ans++;
        }
    }
    return ans;
}

练习：

种花问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public boolean canPlaceFlowers(int[] flowerbed, int n) {
    int ans = 0;
    for (int i = 0; i < flowerbed.length; i++) {
        if (flowerbed[i] == 1) {
            continue;
        }
        if (i - 1 >= 0 && flowerbed[i - 1] == 1) {
            continue;
        }
        if (i + 1 < flowerbed.length && flowerbed[i + 1] == 1) {
            continue;
        }
        flowerbed[i] = 1;
        ans++;
    }
    return ans >= n;
}

划分字母区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public List<Integer> partitionLabels(String s) {
    List<Integer> res = new LinkedList<>();
    for (int i = 0; i < s.length();) {
        int startPoint = i;
        for (int curPoint = i; i <= curPoint; i++) {
            for (int j = s.length() - 1; j > curPoint; j--) {
                if (s.charAt(j) == s.charAt(i)) {
                    curPoint = j;
                    break;
                }
            }
        }
        res.add(i - startPoint);
    }
    return res;
}

P1223 排队接水

贪心 + 排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
package luogu;

import java.util.Arrays;
import java.util.Scanner;

public class p1223 {
    public static class Time implements Comparable<Time> {
        int index;
        int value;

        public Time(int index, int value) {
            this.index = index;
            this.value = value;
        }

        @Override
        public int compareTo(Time time) {
            return this.value - time.value;
        }
    }

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        Time[] times = new Time[n];
        for (int i = 0; i < n; i++) {
            times[i] = new Time(i, in.nextInt());
        }
        in.close();

        Arrays.sort(times);
        long ans = 0;
        for (int i = 0; i < n; i++) {
            System.out.print(Integer.toString(times[i].index + 1) + " ");
            ans += times[i].value * (n - i - 1);
        }
        System.out.println();
        System.out.printf("%.2f\n", (double) ans / n);
    }

}

[P1090 [NOIP 2004 提高组] 合并果子](P1090 [NOIP 2004 提高组] 合并果子)

贪心 + 堆 + 优先队列